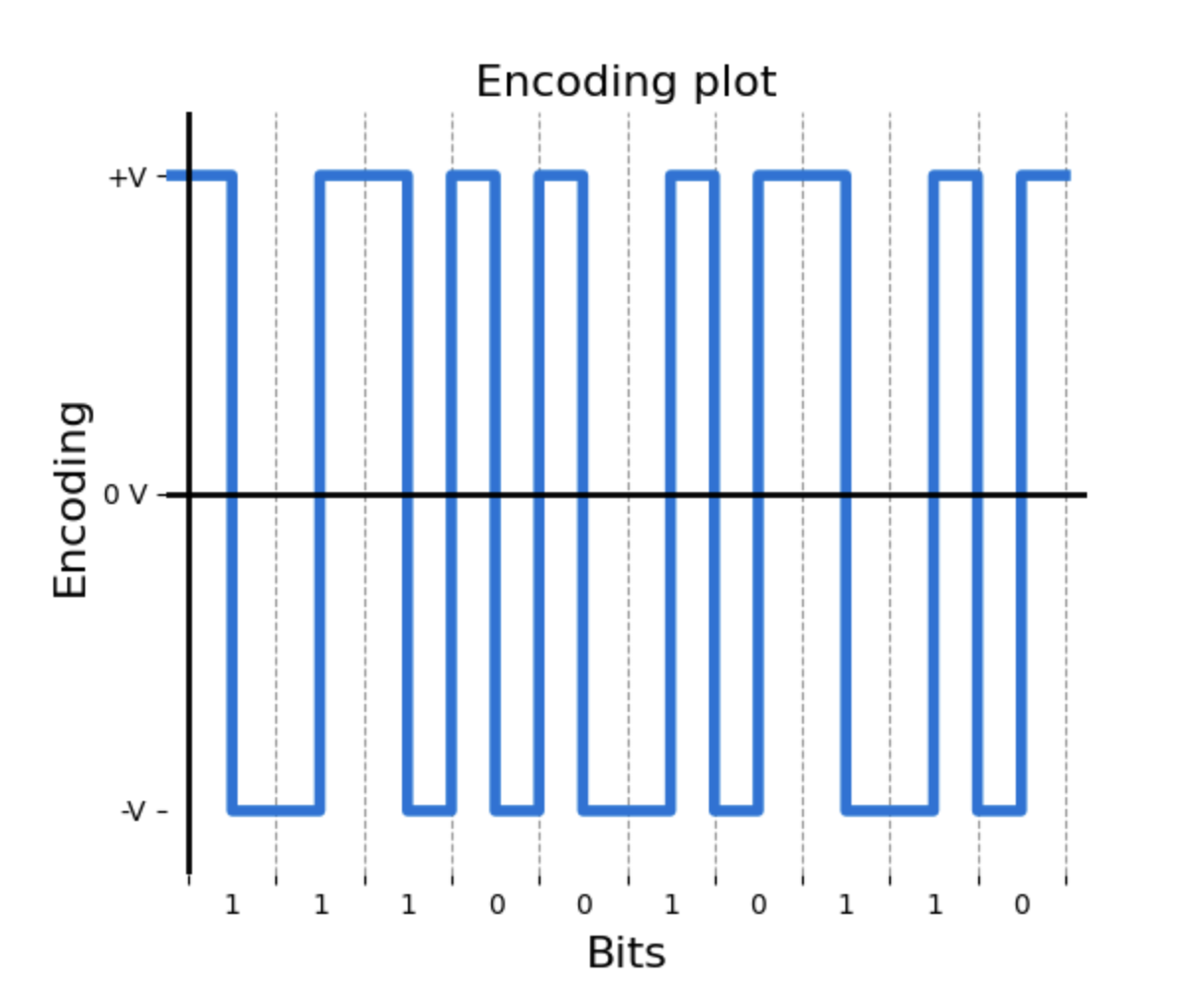
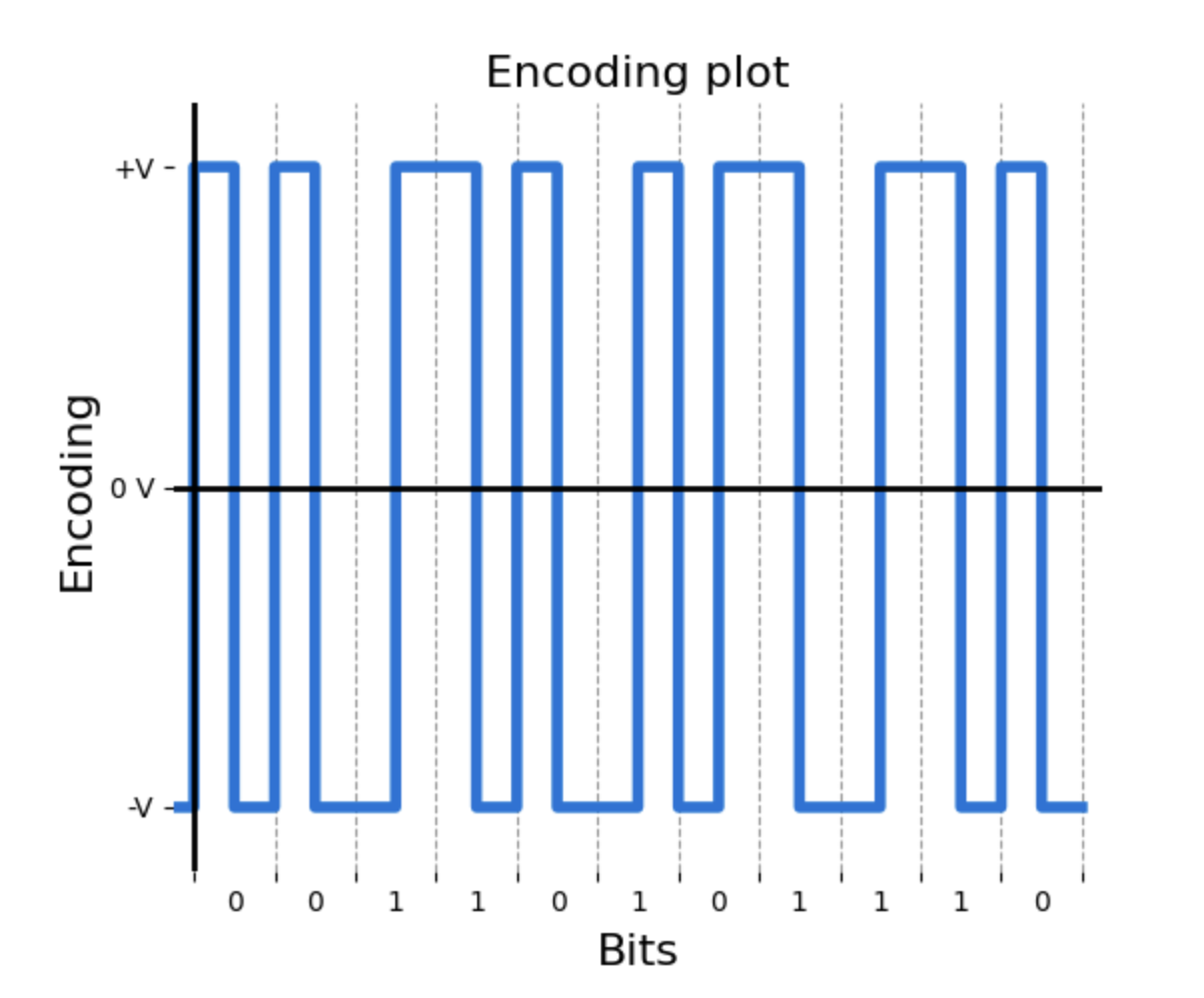
This page covers the Differential Manchester encoding scheme, the second of the biphasic coding schemes that we'll discuss. Just like in the Manchester scheme, the representation of bits is done through transitions between two non-null voltage levels (+V and -V) at the midpoint of each bit period.
Unlike its sibling though, the Differential Manchester encoding does need to know which was the previous bit in order to know the representation of the current bit. This is because one particular feature of this scheme: the bit itself determines whether there's a transition at the beginning of the bit period or not.
The logic for this scheme is as follows: a bit '0' is represented by a transition at the beginning of the bit period, while a bit '1' is represented by no transition at the beginning of the bit period. In both cases, a transition is guaranteed to occur at the midpoint of the bit period (which, as we mentioned before, is a characteristic of the biphasic family of schemes).
Since a bit '0' will cause a transition at the beginning of the bit period, the form that the signal takes will depend on the state it was in at the end of the previous bit. That's the reason why it's necessary to know the shape of signal up to that point.
Like the Manchester scheme, the Differential Manchester encoding inherits the benefits that come with the frequent transitions in the signal, such as better synchronization and a greater resilience to polarity inversion errors than, for example, the unipolar schemes. On the downside, it also inherits biphasic schemes' requirement of a higher bandwidth, and it is, indeed, slightly more complex to implement than the Manchester scheme.
Below are a few examples of the Differential Manchester scheme.